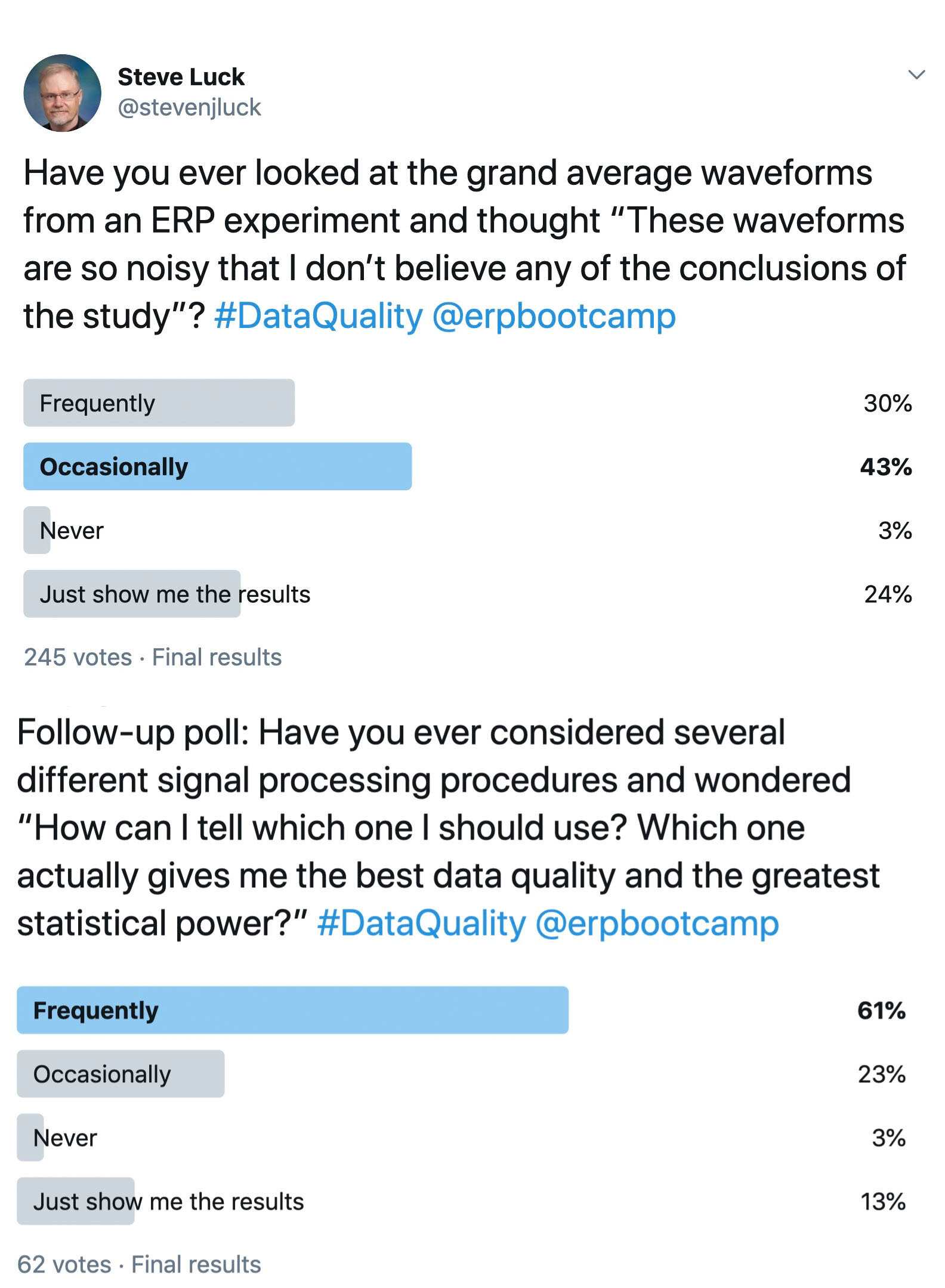
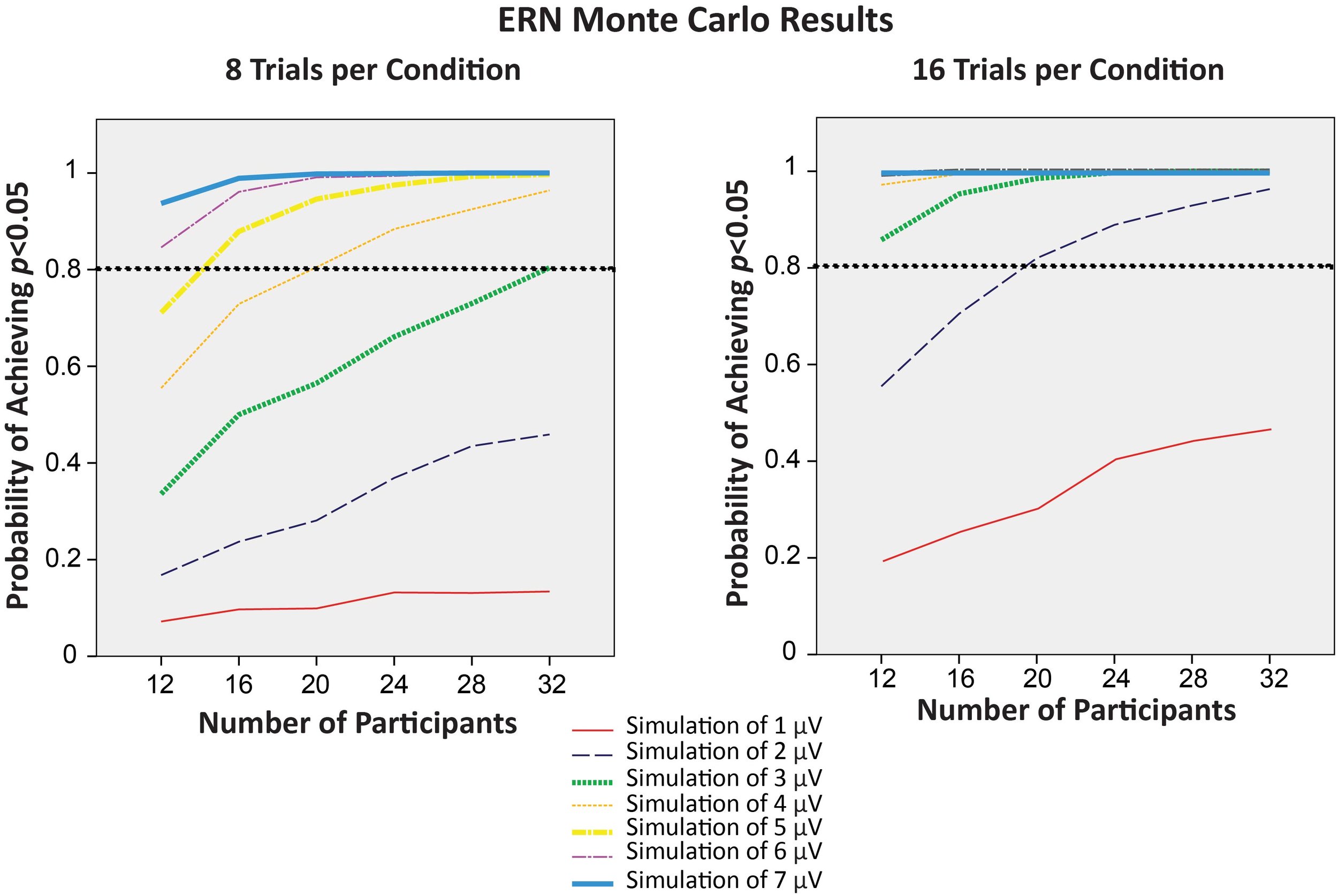
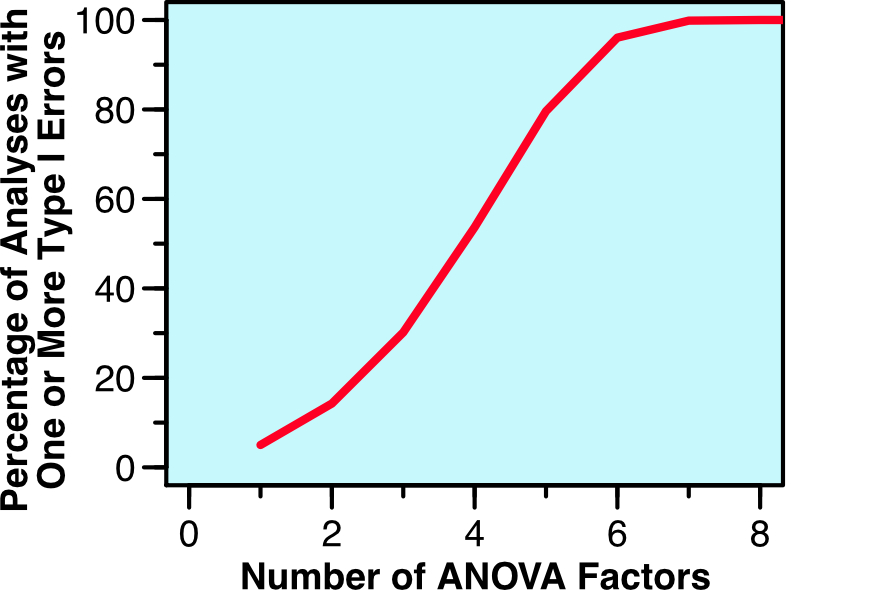
Things are more complicated in most psychology experiments, where there are (at least) two distinct sources of variability in a given experiment: true differences among participants (called the true score variance) and measurement imprecision. However, in a typical experiment, it is not obvious how to separately quantify the true score variance from the measurement imprecision. For example, if you measure a dependent variable once from N participants, and you look at the variance of those values, the result will be the sum of the true score variance and the variance due to measurement error. These two sources of variance are mixed together, and you don’t know how much of the variance is a result of measurement imprecision.
Imagine, however, that you’ve measured the dependent variable twice from each subject. Now you could ask how close the two measures are to each other. For example, if we take our original simple RT experiment, we could get the mean RT from the odd-number trials and the mean RT from the even-numbered trials in each participant. If these two scores were very close to each other in each participant, then we would say we have a precise measure of mean RT. For example, if we collected 2000 trials from each participant, resulting in 1000 odd-numbered trials and 1000 even-numbered trials, we’d probably find that the two mean RTs for a given subject were almost always within 10 ms of each other. However, if collected only 20 trials from each participant, we would see big differences between the mean RTs from the odd- and even-numbered trials. This makes sense: All else being equal, mean RT should be a more precise measure if it’s based on more trials.
In a general sense, we’d like to say that mean RT is a more reliable measure when it’s based on more trials. However, as the first part of this blog post demonstrated, typical psychometric approaches to quantifying reliability are also impacted by the range of values in the population and not just the precision of the measure itself: Dr. Sloppy and Dr. Careful were measuring mean RT with equal precision, but split-half reliability was greater for Dr. Careful than for Dr. Sloppy because there was a greater range of mean RT values in Dr. Sloppy’s study. This is because split-half reliability does not look directly at how similar the mean RTs are for the odd- and even-numbered trials; instead, it involves computing the correlation between these values, which in turn depends on the range of values across participants.
How, then, can we formally quantify precision in a way that does not depend on the range of values across participants? If we simply took the difference in mean RT between the odd- and even-numbered trials, this score would be positive for some participants and negative for others. As a result, we can’t just average this difference across participants. We could take the absolute value of the difference for each participant and then average across participants, but absolute values are problematic in other ways. Instead, we could just take the standard deviation (SD) of the two scores for each person. For example, if Participant #1 had a mean RT of 515 ms for the odd-numbered trials and a mean RT of 525 ms for the even-numbered trials, the SD for this participant would be 7.07 ms. SD values are always positive, so we could average the single-participant SD values across participants, and this would give us an aggregate measure of the precision of our RT measure.
The average of the single-participant SDs would be a pretty good measure of precision, but it would underestimate the actual precision of our mean RT measure. Ultimately, we’re interested in the precision of the mean RT for all of the trials, not the mean RT separately for the odd- and even-numbered trials. By cutting the number of trials in half to get separate mean RTs for the odd- and even-numbered trials, we get an artificially low estimate of precision.
Fortunately, there is a very familiar statistic that allows you to quantify the precision of the mean RT using all of the trials instead of dividing them into two halves. Specifically, you can simply take all of the single-trial RTs for a given participant in a given condition and compute the standard error of the mean (SEM). This SEM tells you what you would expect to find if you computed the mean RT for that subject in each of an infinite number of sessions and then took the SD of the mean RT values.
Let’s unpack that. Imagine that you brought a single participant to the lab 1000 times, and each time you ran 50 trials and took the mean RT of those 50 trials. (We’re imagining that the subject’s performance doesn’t change over repeated sessions; that’s not realistic, of course, but this is a thought experiment so it’s OK.) Now you have 1000 mean RTs (each based on the average of 50 trials). You could take the SD of those 1000 mean RTs, and that would be an accurate way of quantifying the precision of the mean RT measure. It would be just like a chemist who weighs a given object 1000 times on a balance and then uses the SD of these 1000 measurements to quantify the precision of the balance.
But you don’t actually need to bring the participant to the lab 1000 times to estimate the SD. If you compute the SEM of the 50 single-trial RTs in one session, this is actually an estimate of what would happen if you measured mean RT in an infinite number of sessions and then computed the SD of the mean RTs. In other words, the SEM of the single-trial RTs in one session is an estimate of the SD of the mean RT across an infinite number of sessions. (Technical note: It would be necessary to deal with the autocorrelation of RT across trials, but there are methods for that.)
Thus, you can use the SEM of the single-trial RTs in a given session as a measure of the precision of the mean RT measure for that session. This gives you a measure of the precision for each individual participant, and you can then just average these values across participants. Unlike traditional measures of reliability, this measure of precision is completely independent of the range of values across the population. If Dr. Careful and Dr. Sloppy used this measure of precision, they would get exactly the same value (because they’re using exactly the same procedure to measure mean RT in a given participant). Moreover, this measure of precision is directly related to the statistical power for detecting differences between conditions (although there is a trick for aggregating the SEM values across participants, as will be detailed in our paper on ERP data quality).
So, if you want to assess the quality of your data in an experimental study, you should compute the SEM of the single-trial values for each subject, not some traditional measure of “reliability.” Reliability is very important for correlational studies, but it’s not the right measure of data quality in experimental studies.
Here’s the bottom line: the idea that “a measure cannot be valid if it is not reliable” is not true for experimentalists (given how reliability is typically operationalized by psychologists), and they should focus on precision rather than reliability.