Why experimentalists should ignore reliability and focus on precision
/It is commonly said that “a measure cannot be valid if it is not reliable.” It turns out that this is not true as these terms are typically defined in psychology. And it also turns out that, although reliability is extremely important in some types of research (e.g., correlational studies of individual differences), it’s the wrong way for most experimentalists to think about the quality of their measures.
I’ve been thinking about this issue for the last 2 years, as my lab has been working on a new method for quantifying data quality in ERP experiments (stay tuned for a preprint). It turns out that ordinary measures of reliability are quite unsatisfactory for assessing whether ERP data are noisy. This is also true for reaction time (RT) data. A couple days ago, Michaela DeBolt (@MDeBoltC) alerted me to a new paper by Hedge et al. (2018) showing that typical measures of reliability can be low even when power is high in experimental studies. There’s also a recent paper on MRI data quality by Brandmaier et al. (2018) that includes a great discussion of how the term “reliability” is used to mean different things in different fields.
Here’s a quick summary of the main issue: Psychologists usually quantify reliability using correlation-based measures such as Cronbach’s alpha. Because the magnitude of a correlation depends on the amount of true variability among participants, these measures of reliability can go up or down a lot depending on how homogeneous the population is. All else being equal, a correlation will be lower if the participants are more homogeneous. Thus, reliability (as typically quantified by psychologists) depends on the range of values in the population being tested as well as the nature of the measure. That’s like a physicist saying that the reliability of a thermometer depends on whether it is being used in Chicago (where summers are hot and winters are cold) or in San Diego (where the temperature hovers around 72°F all year long).
One might argue that this is not really what psychometricians mean when they’re talking about reliability (see Li, 2003, who effectively redefines the term “reliability” to capture what I will be calling “precision”). However, the way I will use the term “reliability” captures the way this term has been operationalized in 100% of the papers I have read that have quantified reliability (and in the classic texts on psychometrics cited by Li, 2003).
A Simple Reaction Time Example
Let’s look at this in the context of a simple reaction time experiment. Imagine that two researchers, Dr. Careful and Dr. Sloppy, use exactly the same task to measure mean RT (averaged over 50 trials) from each person in a sample of 100 participants (drawn from the same population). However, Dr. Careful is meticulous about reducing sources of extraneous variability, and every participant is tested by an experienced research assistant at the same time of day (after a good night’s sleep) and at the same time since their last meal. In contrast, Dr. Sloppy doesn’t worry about these sources of variance, and the participants are tested by different research assistants at different times of day, with no effort to control sleepiness or hunger. The measures should be more reliable for Dr. Careful than for Dr. Sloppy, right? Wrong! Reliability (as typically measured by psychologists) will actuallybe higher for Dr. Sloppy than for Dr. Careful (assuming that Dr. Sloppy hasn’t also increased the trial-to-trial variability of RT).
To understand why this is true, let’s take a look at how reliability would typically be quantified in a study like this. One common way to quantify the reliability of the RT measure is the split-half reliability. (There are better measures of reliability, but they all lead to the same problem, and split-half reliability is easy to explain.) To compute the split-half reliability, the researchers divide the trials for each participant into odd-numbered and even-numbered trials, and they calculate the mean RT separately for the odd- and even-numbered trials. This gives them two values for each participant, and they simply compute the correlation between these two values. The logic is that, if the measure is reliable, then the mean RT for the odd-numbered trials should be pretty similar to the mean RT for the even-numbered trials in a given participant, so individuals with a fast mean RT for the odd-numbered trials should also have a fast mean RT for the even-numbered trials, leading to a high correlation. If the measure is unreliable, however, the mean RTs for the odd- and even-numbered trials will often be quite different for a given participant, leading to a low correlation.
However, correlations are also impacted by the range of scores, and the correlation between the mean RT for the odd- versus even-numbered trials will end up being greater for Dr. Sloppy than for Dr. Careful because the range of mean RTs is greater for Dr. Sloppy (e.g., because some of Dr. Sloppy’s participants are sleepy and others are not). This is illustrated in the scatterplots below, which show simulations of the two experiments. The experiments are identical in terms of the precision of the mean RT measure (i.e., the trial-to-trial variability in RT for a given participant). The only thing that differs between the two simulations is the range of true mean RTs (i.e., the mean RT that a given participant would have if there were no trial-by-trial variation in RT). Because all of Dr. Careful’s participants have mean RTs that cluster closely around 500 ms, the correlation between the mean RTs for the odd- and even-numbered trials is not very high (r=.587). By contrast, because some of Dr. Sloppy’s participants are fast and others are slow, the correlation is quite good (r=.969). Thus, simply by allowing the testing conditions to vary more across participants, Dr. Sloppy can report a higher level of reliability than Dr. Careful.
Keep in mind that Dr. Careful and Dr. Sloppy are measuring mean RT in exactly the same way. The actual measure is identical in their studies, and yet the measured reliability differs dramatically across the studies because of the differences in the range of scores. Worse yet, the sloppy researcher ends up being able to report higher reliability than the careful researcher.
Let’s consider an even more extreme example, in which the population is so homogeneous that every participant would have the same mean RT if we averaged together enough trials, and any differences across participants in observed mean RT are entirely a result of random variation in single-trial RTs. In this situation, the split-half reliability would have an expected value of zero. Does this mean that mean RT is no longer a valid measure of processing speed? Of course not—our measure of processing speed is exactly the same in this extreme case as in the studies of Dr. Careful and Dr. Sloppy. Thus, a measure can be valid even if it is completely unreliable (as typically quantified by psychologists).
Here’s another instructive example. Imagine that Dr. Careful does two studies, one with a population of college students at an elite university (who are relatively homogeneous in age, education, SES, etc.) and one with a nationally representative population of U.S. adults (who vary considerably in age, education, SES, etc.). The range of mean RT values will be much greater in the nationally representative population than in the college student population. Consequently, even if Dr. Careful runs the study in exactly the same way in both populations, the reliability will likely be much greater in the nationally representative population than in the college student population. Thus, reliability (as typically measured by psychologists) depends on the range of scores in the population being measured and not just on the properties of the measure itself. This is like saying that a thermometer is more reliable in Chicago than in San Diego simply because the range of temperatures is greater in Chicago.
Example of an Experimental Manipulation
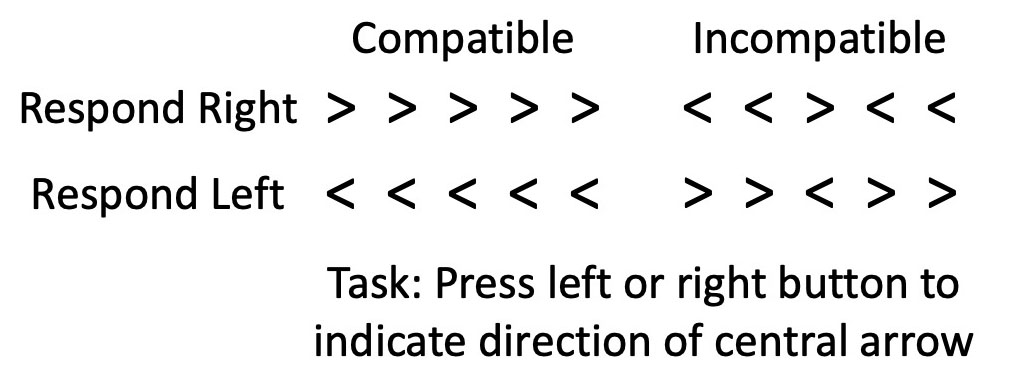
Now let’s imagine that Dr. Careful and Dr. Sloppy don’t just measure mean RT in a single condition, but they instead test the effects of a within-subjects experimental manipulation. Let’s make this concrete by imagining that they conduct a flankers experiment, in which participants report whether a central arrow points left or right while ignoring flanking stimuli that are either compatible or incompatible with the central stimulus (see figure to the right). In a typical study, mean RT would be slowed on the incompatible trials relative to the compatible trials (a compatibility effect).
If we look at the mean RTs in a given condition of this experiment, we will see that the mean RT varies from participant to participant much more in Dr. Sloppy’s version of the experiment than in Dr. Careful’s version (because there is more variation in factors like sleepiness in Dr. Sloppy’s version). Thus, as in our original example, the split-half reliability of the mean RT for a given condition will again be higher for Dr. Sloppy than for Dr. Careful. But what about the split-half reliability of the flanker compatibility effect? We can quantify the compatibility effect as the difference in mean RT between the compatible and incompatible trials for a given participant, averaged across left-response and right-response trials. (Yes, there are better ways to analyze these data, but they all lead to the same conclusions about reliability.) We can compute the split-half reliability of the compatibility effect by computing it twice for every subject—once for the odd-numbered trials and once for the even-numbered trials—and calculating the correlation between these values.
The compatibility effect, like the raw RT, is likely to vary according to factors like the time of day, so the range of compatibility effects will be greater for Dr. Sloppy than for Dr. Careful. And this means that the split-half reliability will again be greater for Dr. Sloppy than for Dr. Careful. (Here I am assuming that trial-to-trial variability in RT is not impacted by the compatibility manipulation and by the time of day, which might not be true, but nonetheless it is likely that the reliability will be at least as high for Dr. Sloppy as for Dr. Careful.)
By contrast, statistical power for determining whether a compatibility effect is present will be greater for Dr. Careful than for Dr. Sloppy. In other words, if we use a one-sample t test to compare the mean compatibility effect against zero, the greater variability of this effect in Dr. Sloppy’s experiment will reduce the power to determine whether a compatibility effect is present. So, even though reliability is greater for Dr. Sloppy than for Dr. Careful, statistical power for detecting an experimental effect is greater for Dr. Careful than for Dr. Sloppy. If you care about statistical power for experimental effects, reliability is probably not the best way for you to quantify data quality.
An Example of Individual Differences
What if Dr. Careful and Dr. Sloppy wanted to look at individual differences? For example, imagine that they were testing the hypothesis that the flanker compatibility effect is related to working memory capacity. Let’s assume that they measure both variables in a single session. Assuming that both working memory capacity and the compatibility effect vary as a function of factors like time of day, Dr. Sloppy will find greater reliability for both working memory capacity and the compatibility effect (because the range of values is greater for both variables in Dr. Sloppy’s study than in Dr. Careful’s study). Moreover, the correlation between working memory capacity and the compatibility effect will be higher in Dr. Sloppy’s study than in Dr. Careful’s study (again because of differences in the range of scores).
In this case, greater reliability is associated with stronger correlations, just as the psychometricians have always told us. All else being equal, the researcher who has greater reliability for the individual measures (Dr. Sloppy in this example) will find a greater correlation between them. So, if you want to look at correlations between measures, you want to maximize the range of scores (which will in turn maximize your reliability). However, recall that Dr. Careful had more statistical power than Dr. Sloppy for detecting the compatibility effect. Thus, the same factors that increase reliability and correlations between measures can end up reducing statistical power when you are examining experimental effects with exactly the same measures. (Also, if you want to look at correlations between RT and other measures, I recommend that you read Miller & Ulrich, 2013, which shows that these correlations are more difficult to interpret than you might think.)
It’s also important to note that Dr. Sloppy would run into trouble if we looked at test-retest reliability instead of split-half reliability. That is, imagine that Dr. Sloppy and Dr. Careful run studies in which each participant is tested on two different days. Dr. Careful makes sure that all of the testing conditions (e.g., time of day) are the same for every participant, but Dr. Sloppy isn’t careful to keep the testing conditions constant between the two session for each participant. The test-retest reliability (the correlation between the measure on Day 1 and Day 2) would be low for Dr. Sloppy. Interestingly, Dr. Sloppy would have high split-half reliability (because of the broad range of scores) but poor test-retest reliability. Dr. Sloppy would also have trouble if the compatibility effect and working memory capacity were measured on different days.
Precision vs. Reliability
Now let’s turn to the distinction between reliability and precision. The first part of the Brandmaier et al. (2018) paper has an excellent discussion of how the term “reliability” is used differently across fields. In general, everyone agrees that a measure is reliable to the extent that you get the same thing every time you measure it. The difference across fields lies in how reliability is quantified. When we think about reliability in this way, a simple way to quantify it would be to obtain the measure a large number of times under identical conditions and compute the standard deviation (SD) of the measurements. The SD is a completely straightforward measure of the “the extent that you get the same thing every time you measure it.” For example, you could use a balance to weigh an object 100 times, and the standard deviation of the weights would indicate the reliability of the balance. Another term for this would be the “precision” of the balance, and I will use the term “precision” to refer to the SD over multiple measurements. (In physics, the SD is typically divided by the mean to get the coefficient of variability, which is often a better way to quantify reliability for measures like weight that are on a ratio scale.)
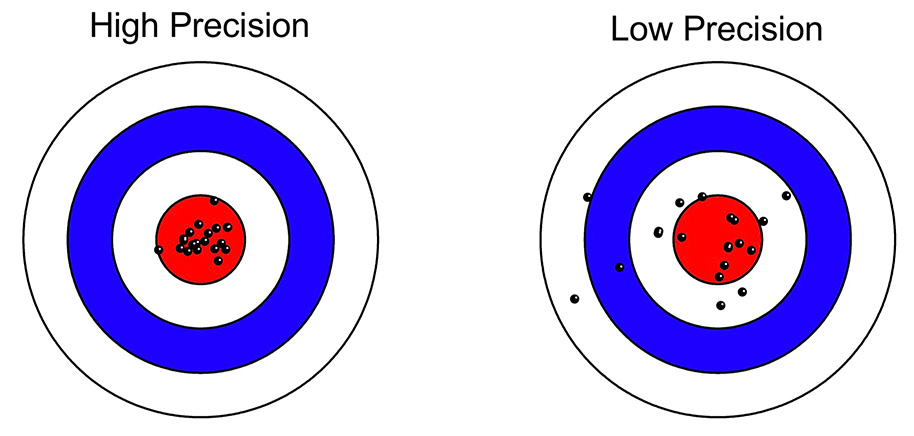
The figure below (from the Brandmaier article) shows what is meant by low and high precision in this context, and you can see how the SD would be a good measure of precision. The key is that precision reflects the variability of the measure around its mean, not whether the mean is the true mean (which would be the accuracy or bias of the measure).
Things are more complicated in most psychology experiments, where there are (at least) two distinct sources of variability in a given experiment: true differences among participants (called the true score variance) and measurement imprecision. However, in a typical experiment, it is not obvious how to separately quantify the true score variance from the measurement imprecision. For example, if you measure a dependent variable once from N participants, and you look at the variance of those values, the result will be the sum of the true score variance and the variance due to measurement error. These two sources of variance are mixed together, and you don’t know how much of the variance is a result of measurement imprecision.
Imagine, however, that you’ve measured the dependent variable twice from each subject. Now you could ask how close the two measures are to each other. For example, if we take our original simple RT experiment, we could get the mean RT from the odd-number trials and the mean RT from the even-numbered trials in each participant. If these two scores were very close to each other in each participant, then we would say we have a precise measure of mean RT. For example, if we collected 2000 trials from each participant, resulting in 1000 odd-numbered trials and 1000 even-numbered trials, we’d probably find that the two mean RTs for a given subject were almost always within 10 ms of each other. However, if collected only 20 trials from each participant, we would see big differences between the mean RTs from the odd- and even-numbered trials. This makes sense: All else being equal, mean RT should be a more precise measure if it’s based on more trials.
In a general sense, we’d like to say that mean RT is a more reliable measure when it’s based on more trials. However, as the first part of this blog post demonstrated, typical psychometric approaches to quantifying reliability are also impacted by the range of values in the population and not just the precision of the measure itself: Dr. Sloppy and Dr. Careful were measuring mean RT with equal precision, but split-half reliability was greater for Dr. Careful than for Dr. Sloppy because there was a greater range of mean RT values in Dr. Sloppy’s study. This is because split-half reliability does not look directly at how similar the mean RTs are for the odd- and even-numbered trials; instead, it involves computing the correlation between these values, which in turn depends on the range of values across participants.
How, then, can we formally quantify precision in a way that does not depend on the range of values across participants? If we simply took the difference in mean RT between the odd- and even-numbered trials, this score would be positive for some participants and negative for others. As a result, we can’t just average this difference across participants. We could take the absolute value of the difference for each participant and then average across participants, but absolute values are problematic in other ways. Instead, we could just take the standard deviation (SD) of the two scores for each person. For example, if Participant #1 had a mean RT of 515 ms for the odd-numbered trials and a mean RT of 525 ms for the even-numbered trials, the SD for this participant would be 7.07 ms. SD values are always positive, so we could average the single-participant SD values across participants, and this would give us an aggregate measure of the precision of our RT measure.
The average of the single-participant SDs would be a pretty good measure of precision, but it would underestimate the actual precision of our mean RT measure. Ultimately, we’re interested in the precision of the mean RT for all of the trials, not the mean RT separately for the odd- and even-numbered trials. By cutting the number of trials in half to get separate mean RTs for the odd- and even-numbered trials, we get an artificially low estimate of precision.
Fortunately, there is a very familiar statistic that allows you to quantify the precision of the mean RT using all of the trials instead of dividing them into two halves. Specifically, you can simply take all of the single-trial RTs for a given participant in a given condition and compute the standard error of the mean (SEM). This SEM tells you what you would expect to find if you computed the mean RT for that subject in each of an infinite number of sessions and then took the SD of the mean RT values.
Let’s unpack that. Imagine that you brought a single participant to the lab 1000 times, and each time you ran 50 trials and took the mean RT of those 50 trials. (We’re imagining that the subject’s performance doesn’t change over repeated sessions; that’s not realistic, of course, but this is a thought experiment so it’s OK.) Now you have 1000 mean RTs (each based on the average of 50 trials). You could take the SD of those 1000 mean RTs, and that would be an accurate way of quantifying the precision of the mean RT measure. It would be just like a chemist who weighs a given object 1000 times on a balance and then uses the SD of these 1000 measurements to quantify the precision of the balance.
But you don’t actually need to bring the participant to the lab 1000 times to estimate the SD. If you compute the SEM of the 50 single-trial RTs in one session, this is actually an estimate of what would happen if you measured mean RT in an infinite number of sessions and then computed the SD of the mean RTs. In other words, the SEM of the single-trial RTs in one session is an estimate of the SD of the mean RT across an infinite number of sessions. (Technical note: It would be necessary to deal with the autocorrelation of RT across trials, but there are methods for that.)
Thus, you can use the SEM of the single-trial RTs in a given session as a measure of the precision of the mean RT measure for that session. This gives you a measure of the precision for each individual participant, and you can then just average these values across participants. Unlike traditional measures of reliability, this measure of precision is completely independent of the range of values across the population. If Dr. Careful and Dr. Sloppy used this measure of precision, they would get exactly the same value (because they’re using exactly the same procedure to measure mean RT in a given participant). Moreover, this measure of precision is directly related to the statistical power for detecting differences between conditions (although there is a trick for aggregating the SEM values across participants, as will be detailed in our paper on ERP data quality).
So, if you want to assess the quality of your data in an experimental study, you should compute the SEM of the single-trial values for each subject, not some traditional measure of “reliability.” Reliability is very important for correlational studies, but it’s not the right measure of data quality in experimental studies.
Here’s the bottom line: the idea that “a measure cannot be valid if it is not reliable” is not true for experimentalists (given how reliability is typically operationalized by psychologists), and they should focus on precision rather than reliability.